Abstract
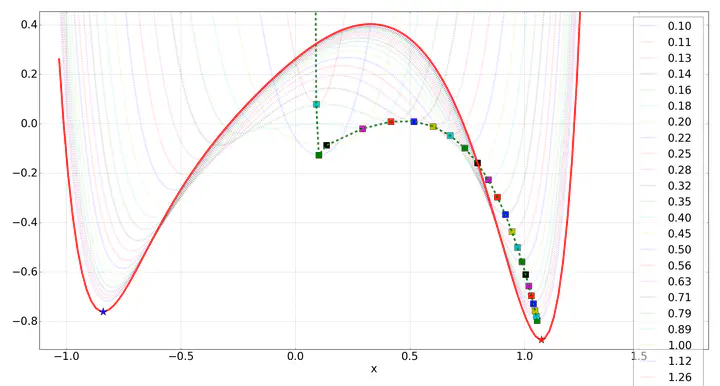
Numerical optimization has been the workhorse powering the success of many machine learning and artificial intelligence tools over the last decade. However, current state-of-the-art algorithms for solving unconstrained non-convex optimization problems in high-dimensional spaces, either suffer from the curse of dimensionality as they rely on sampling, or get stuck in local minima as they rely on gradient-based optimization. We present a new graduated optimization method based on the optimization of the integral of the cost function over a region, which is incrementally shrunk towards a single point, recovering the original problem. We focus on the optimization of polynomial functions, for which the integral over simple regions (e.g. hyperboxes) can be computed efficiently. We show that this algorithm is guaranteed to converge to the global optimum in the simple case of a scalar decision variable. While this theoretical result does not extend to the multi-dimensional case, we empirically show that our approach outperforms state- of-the-art algorithms (BFGS and CMA-ES) in high dimensions (up to 72 decision variables) when tested on sparse polynomial functions with a high number of local minima.