Abstract
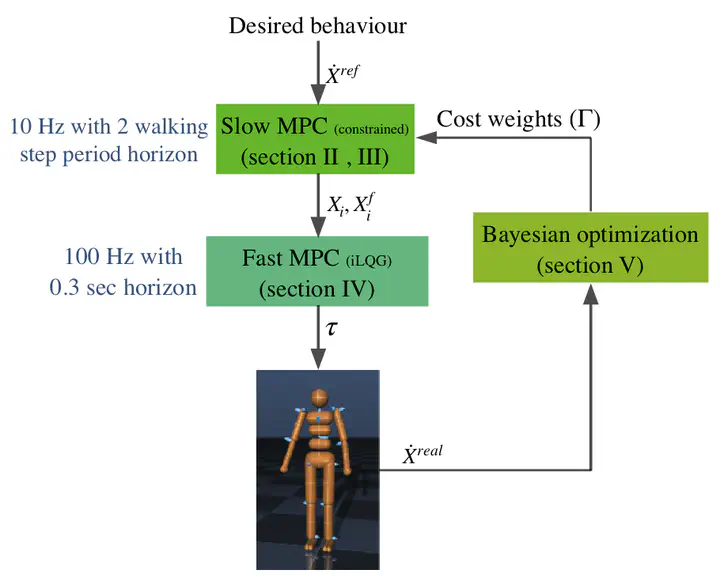
Model predictive control (MPC) has shown great success for controlling complex systems, such as legged robots. However, when closing the loop, the performance and feasibility of the finite horizon optimal control problem (OCP) solved at each control cycle are not guaranteed anymore. This is due to model discrepancies, the effect of low-level controllers, uncertainties, and sensor noise. To address these issues, we propose a modified version of a standard MPC approach used in legged locomotion with viability (weak forward invariance) guarantees. In this approach, instead of adding a (conservative) terminal constraint to the problem, we propose to use the measured state projected to the viability kernel in the OCP solved at each control cycle. Moreover, we use past experimental data to find the best cost weights, which measure a combination of performance, constraint satisfaction robustness, or stability (invariance). These interpretable costs measure the tradeoff between robustness and performance. For this purpose, we use Bayesian optimization to systematically design experiments that help efficiently collect data to learn a cost function leading to robust performance. Our simulation results with different realistic disturbances (i.e., external pushes, unmodeled actuator dynamics, and computational delay) show the effectiveness of our approach to create robust controllers for humanoid robots.