Robust Satisfaction of Joint Position and Velocity Bounds in Discrete-Time Acceleration Control of Robot Manipulators

Abstract

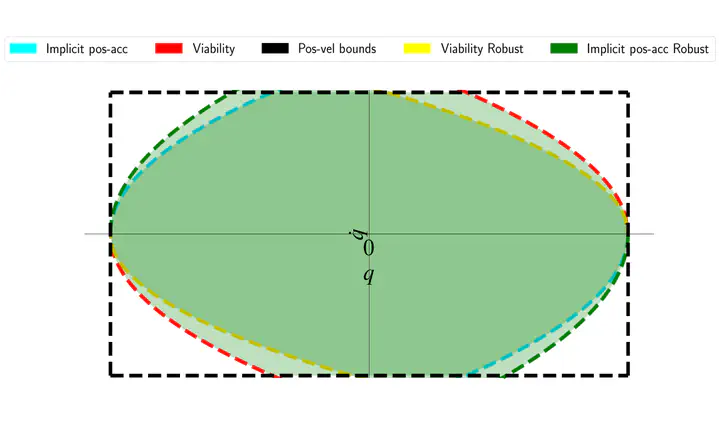
This paper deals with the robust control of fully-actuated robots subject to joint position, velocity and acceleration bounds. Robotic systems are subject to disturbances, which may arise from modeling errors, sensor noises or communication delays. This work presents mathematical and computational tools to ensure the robust satisfaction of joint bounds in the control of robot manipulators. We consider a system subject to bounded additive disturbances on the control inputs, with constant joint position, velocity and acceleration bounds. We compute the robust viability kernel, which is the set of states such that, starting from any such state, it is possible to avoid violating the constraints in the future, despite the presence of disturbances. Then we develop an efficient algorithm to compute the range of feasible accelerations that allow the state to remain inside the robust viability kernel. Our derivation ensures the continuous-time robust satisfaction of the joint bounds, while considering the discrete-time nature of the control inputs. Tests are performed in simulation with a single joint and a 6-DOF robot manipulator, demonstrating the effectiveness of the proposed approach compared to other state-of-the-art methods.